Why do things happen?

Things happen because they are likely. In other words, things happen because entropy increases. Nothing happens only in systems that are at their maximum possible entropy already—we say they are in thermodynamic equilibrium. However, since the overall universe is still far from thermodynamic equilibrium, it is likely that any such system will eventually be subject to some outside influence that takes it out of this equilibrium, so that things can happen within it again.

Systems where things happen belong to one of two categories.

1. Many systems simply have an internal increase in entropy all the time. For example, a solid or liquid left alone in space would have this, for example, it would lose more and more particles to the gaseous state over time (gasses have higher entropy than liquids or solids, generally speaking).
2. Other systems, including many highly interesting systems like humans and their economic activity, all living beings, and computers, sometimes achieve self-organization (See Postulate 6 of Halbe’s Razor). This means there are times where they lose entropy internally, which is “paid for” by a higher increase of entropy outside of the system, so that in total, the universe gains entropy.

To have the ability to be self-organizing, a system needs to contain a lot of information, that means its entropy needs to be a lot lower than it would be if all its particles were randomly mixed. But this is a necessary, not a sufficient condition. A system with high information content can still be not self-organizing. All solids and liquids are not yet gaseous, they thus contain more information than they could, but they slowly lose it to decay. But systems with an even higher information content which are not self-organizing normally are the result of self-organizing processes in the past. For example, a painting, book or solid state disk that was buried decades ago is no longer part of a self-organizing system, it still has a high information content, but its entropy is always increasing (it is decaying). Similarly, a cell or multi-cellular organism that has died still contains a lot of information, but is decaying. 

To make sure a system is still self-organizing, we have to observe it organize itself, i.e. lower its entropy between an earlier and a later point in time. But even for such systems, there is always a chance to fail at organizing itself. This is because the universe is fundamentally stochastic (see Postulate 4), and noise and randomness can prevent self-organization from occurring. In this sense, systems with the ability to self-organize can be compared to a Galton Board, where chance will pick what happens: Self-organization or internal entropy increase. This is in contrast to systems without the ability to self-organize, where we always see an internal entropy increase, and those who have already reached maximum entropy (thermodynamic equilibrium), in which nothing changes.

Since all of this is stochastic, Halbe’s Razor calls all changes in between two points in time “occurrences” (Postulate 2).

Figure 1 displays these three categories of occurrences.

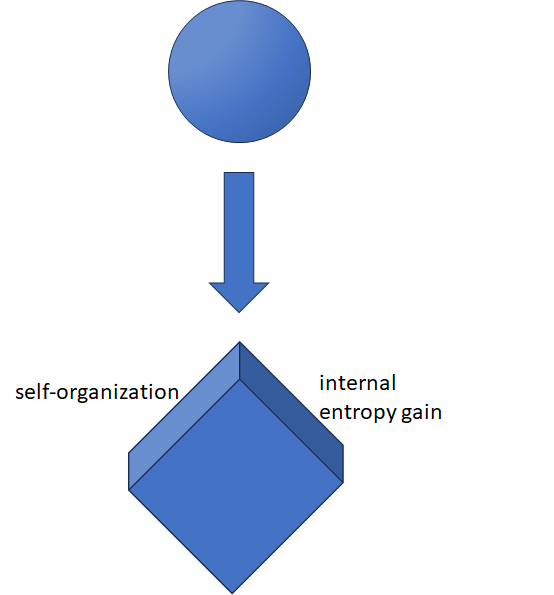
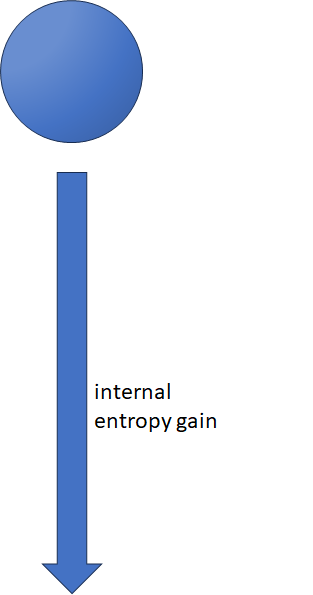
Figure 1: Systems categorized by which occurrences are possible in them. The movement of the ball represents change in a system. In a., it will hit the peg and randomly go left or right. In b., it will go on unimpeded to an increase in internal entropy in the system. In c., it doesn’t move (nothing changes).

If chance makes a system with the ability to self-organize fail to do so (the ball goes to the right), it makes the system lose information content, which makes more such failures likelier in the future, and if this happens too often in a row, it can lose the ability to self-organize. On the other hand, if self-organization succeeds through reasons just as random, it gains more information and thus can reverse former failures of self-organization, as well as make more self-organization likelier in the future. Figure 2 demonstrates this.

In self-organizing systems, several outcomes are possible if they are very similar in their entropy production. They need to be similar because anything else would make them too unlikely. If several are possible, each will have a probability and random chance will decide between them, with the trivial internal entropy increase (failure to self-organize) always another possible outcome with a certain probability dependent on the information content, as described above. Figure 3 demonstrates this for three possible cases in addition to this trivial case.

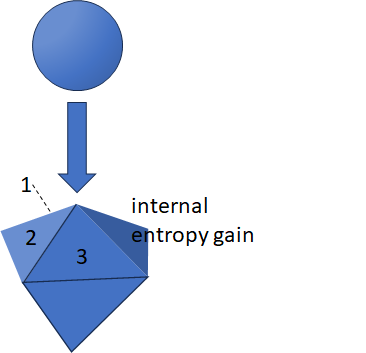
Systems very rich in information (like a human brain) will have more different ways to reach very similar levels of total entropy increase in the universe, therefore the three-dimensional Galton board peg according to Figure 3 will have more sides. Simpler systems (like those commonly described as “deterministic”, like a computer solving a simple calculation), will have fewer such possible outcomes.

Additionally, building up on Figure 2, whenever an outcome occurs at t₀, it will result in different possible outcomes in the future, each with their own new probability. Just as in Figure 2, hitting the “internal entropy gain” side will result in it becoming likelier in the future. But more complex than in Figure 2, hitting any of the sides will also reshape the entire peg at t₁, it can no longer be visualized with a simple rotation. This should make clear that it is complicated to talk about such concrete outcomes instead of staying with what is described in Figure 2. Quite often, the level of complexity shown is sufficient, and a many texts on this website will use it. But a text about epistemology will talk about this in greater detail.

Summary

Regardless of whether the system is self-organizing or not, things happen because they are likelier than other possible things. In systems which are not self-organizing at the time, this is because they mean the highest possible increase in entropy within the system. In self-organizing systems, it is because the sum of internal they mean an increase in entropy in the universe that is higher than a simple increase in entropy within the given system would be because it means such a high increase in entropy outside of the system. For only that way, the latter thing will be likelier than the simple increase within the system, since total entropy increase is a measure of how likely something is. The more similar the total entropy production of two mutually exclusive potential occurrences is, the more similar is their chance to occur. If one such potential event has much less total entropy production than the other, it is for all intents and purposes impossible because of the law of large numbers and should not even be called a potential event.

We now know why things happen. The implications of that will be discussed in other texts on this website.

1 comment